- 15 December, 2015
- Elections

Linear Regression
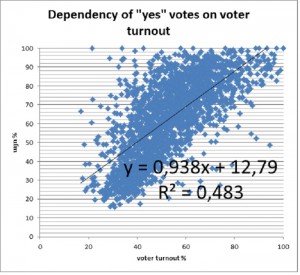
The graph shows the dependency of the percentage of people who voted “yes” on the percentage of voter turnout. The dots correspond to the preliminary results from all the 1997 polling stations. The percentage of “yes” votes” is high in those polling stations where high turnout was recorded. Regression line coefficient k=0,938: Ideally, we should have k=0, that is, the result should not depend on voter turnout. If ballot stuffing does not occur, on average we should have the same result in all the polling stations irrespective of voter turnout. In case of k>0, we deal with ballot stuffing. In our case, on average the percentage of “yes” votes is in explicit proportion to the percentage of voter turnout. That is also substantiated by the fact that in case of double voting, ballot stuffing and falsification of results protocols, not only “yes” votes increase, but also the voter turnout becomes higher.
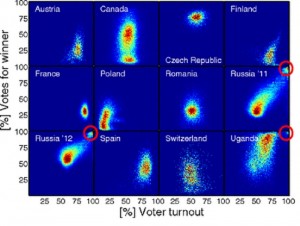
Some opponents of this methodology claim that the active participation is related to the fact that the “yes” proponents were more eager to go to the polling stations and vote. However, we do not observe such tendencies in Switzerland, where referendums are held most frequently. Below you can find respective graphs of elections in different countries. They are aimed at statistical revelation of election fraud. Our graph is similar to those of Uganda and Russia.
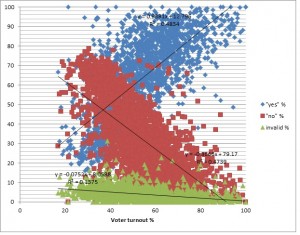
There is one more interesting observation: as the percentage of “no” votes decreases along with increase of voter turnout, the percentage of invalid/spoilt ballots also decreases. That is, the lower the voter turnout, the lower the percentage of invalid ballots. This allows us to assume that in the polling stations where low voter turnout was registered, and where it was not possible to add “yes” votes, the method of making “no” ballots invalid has been applied.
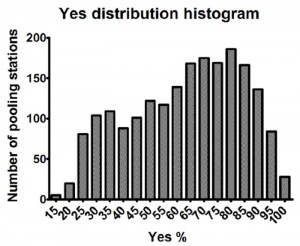
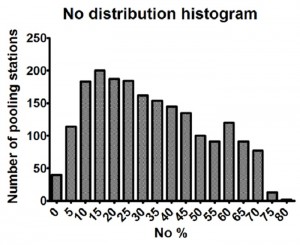
The distribution of percentage of “Yes” votes does not represent normal distribution.
The concept of normal distribution in statistics. Normal or Gaussian distribution represents such a distribution of values in case of which those values are probable (among different values) which are close to the mean of all the values. Moreover, the larger the deviation of the value is from the mean, the smaller the possibility of encountering it. In case of such distribution, we can say that all the values are subject to a common law. Roughly speaking, in our case the distribution will be normal, if 63% “yes” is registered in the largest number of polling stations. In other words, the most probable result should coincide with the average index. The polling stations that registered larger or smaller number of “yes” votes compared to the mean (63%) should be smaller in number. Moreover, the larger the difference from the mean, the smaller the probability should be. If distribution is not normal, it is assumed that the principle of randomness has been violated. In our particular case, the latter means that voting irregularities (election fraud) have occurred. There are tests that allow us to check the normality of distribution. Those are Kolmogorov-Smirnov, D’Agostino-Pierson and Shapiro-Wilkie tests. In our case, all the test results indicate that the distribution is not normal. It is worth mentioning that there are numerous precedents of checking the presence of election fraud in this specific way. Particularly, normal distribution is observed in elections in Switzerland and Canada. However, we cannot say the same about elections in Russia.
Thus, the histogram shown in the picture below clearly shows that 80% is the most recurrent one, which can be found in 186 polling stations.
A second peak can also be observed in the histogram – 35%, which has been found in 109 polling stations. Hence, we can assume that we have two peaks, and, consequently, two distributions and two patterns. If we give a very rough assessment, we can speculate that the first pattern -35% expressed the true picture, and the second pattern corresponds to rigged polling stations, where up to 80% was rigged. As a result, the mean value in the republic has resulted to be 63%.
The same two peaks can also be observed in the histogram of “no” votes. The first peak is observed on 15% (200 polling stations), the second peak – on 60% (120 polling stations).
Such “double hump” histograms can be observed in countries where different regions have serious differences. For instance, in Belgium, French-speaking and Flemish-speaking regions are largely different and, hence, such an election outcome is possible. Another example is Spain, where two regions want to secede and, hence, display different tendencies during elections. Nevertheless, all the marzes (regions) of Armenia have the same national, religious, linguistic and social structure. Armenia itself is a unitary state. In other words, there is no border in our country beyond which there are people who have radically different views. Consequently, we can exclude the generation of such “double-peaked” histograms of elections without falsifications.
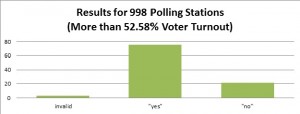
Results for Polling Stations with Low Voter Turnout
It is known that the number of adult population in the republic is less than the number included in the electoral list by as much as 20-25%. Consequently, the polling stations that have registered more than 60-70% voter turnout should arouse doubt. For that reason, a widespread method of checking is the comparison of results by polling stations with low turnout and those with high turnout. If the elections have been fair, the same result should be registered in polling stations with low voter turnout as well.
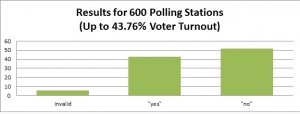
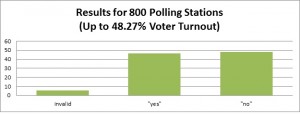
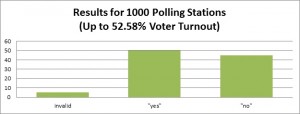
However, we have the following picture: in 600 polling stations with the lowest voter turnout, “yes” has got 43%, and “no” has got 52%. In 800 polling stations with the lowest voter turnout, “yes” has got 46% and “no” has got “48%”. In 1000 polling stations with the lowest voter turnout, “yes” has got 49% and “no” has got 45%. And in the 998 polling stations with the highest voter turnout, “yes” has got 75% and “no” has got 22%.
Such a picture can have only one explanation: in the polling stations where the “yes” proponents have had an opportunity to make an evidently false results protocol (that is, de facto there was no representative of “no” in these polling stations), a few techniques have been used – not only have “no” votes been moved to “yes” votes, but also the ballots of citizens who did not vote were attributed to the “yes” votes.
The point is that by the current legislation, persons who have not been present in the polling station, cannot demand recounting of votes. Hence, if all those who are present in the polling station are accomplices of the falsification, there is no possibility for recounting to take place. As a result of that circumstance, a possibility arsies to add all the possible ballots to the “yes” votes in the polling stations where no proper control was ensured. As a result, very high turnout and an extremely high number of “yes” votes is “registered” in these polling stations (which, naturally, has nothing to do with the expression of will of the citizens).
Union of Informed Citizens


 Հայ
Հայ Рус
Рус